Auteur·es : Frédéric Audard, Grégoire Le Campion, Julie Pierson
Evaluateurs : Hélène Mathian, Thierry Feuillet
Editeur·rices : Ronan Ysebaert, Marion Gentilhomme

Résumé

Cet article présente la réalisation d’une analyse de données à l’aide de la régression géographique pondérée ou GWR (Geographical Weighted Regression). La modélisation statistique dite “classique” présente des risques élevés lorsqu’on souhaite traiter des données spatiales. Des phénomènes de dépendance spatiale, des problèmes d’échelles d’application, des effets de contexte, ainsi qu’une forme d’hétérogénéité spatiale peuvent apparaître et compromettre les analyses effectuées, et engendrer des interprétations tronquées voire inexactes. Souvent ignorées, ces dimensions spatiales ne peuvent pas être considérées comme un simple aléa.

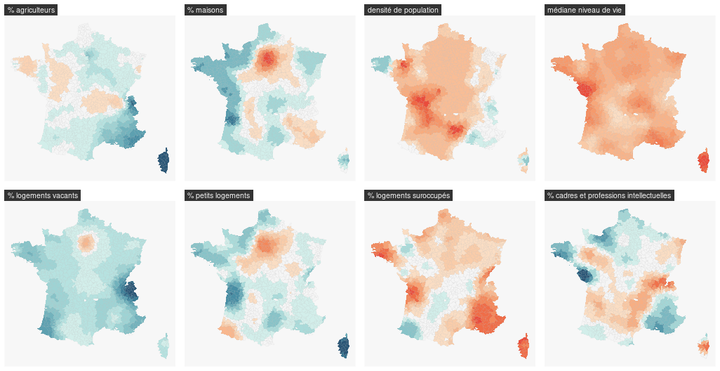
L’objectif de cet article est de vous présenter des méthodes et leurs applications qui vous permettront d’étudier concrètement les effets des dimensions spatiales des données. Il s’agira d’une part de caractériser la structure spatiale de données attributaires liées à des entités spatiales ; et d’autre part de mesurer l’effet statistique de l’information spatiale dans un modèle de régression visant à déterminer les facteurs explicatifs d’un phénomène.

L’analyse présentée ici a pour objectif d’être reproductible : les données spatiales utilisées proviennent de la base ADMIN-EXPRESS de l’Institut national de l’information géographique et forestière (IGN) ; les données statistiques, quant à elles, ont été construites à partir de la base des notaires de France, complétées par des données de l’Institut national de la statistique et des études économiques (INSEE) pour les variables explicatives.

Citation