Archeofrag, an R package for Refitting and Spatial Analysis in Archaeology
Introduction
Les archéologues traitent de phénomènes spatiaux à plusieurs échelles d’analyse ; par conséquent, leur capacité à distinguer des entités spatiales est fondamentale. Lors d’une fouille, des objets sont découverts dans différents types d’unités spatiales, tels que des couches stratigraphiques, des fosses, des foyers ou des espaces habités. Ces unités spatiales sont tout sauf des données brutes : l’identification et la détermination de leurs limites sont le résultat conjoint de différentes méthodes d’investigation : pour n’en citer que quelques-unes, l’observation de directe sur terrain, la géoarchéologie, la sédimentologie, et l’étude des « remontages » archéologiques. Les fragments concernés par ces « remontages » ont appartenu au même objet jusqu’à un moment donné dans le passé. Plus précisément, les archéologues déduisent les relations de connexion qui ont existé entre ces fragments à partir de la symétrie et de la possibilité d’un contact suffisamment étendu des surfaces de deux fragments, lesquels peuvent alors être physiquement ajustés l’un à l’autre (les fragments « remontent »). Le terme de « connexion » est ici utilisé comme un raccourci commode pour désigner la relation de connexion qui existait dans le passé entre deux zones d’un objet avant qu’il ne soit brisé en fragments. L’analyse archéologique des remontages a plusieurs objectifs :
- reconstruire physique les objets ou déterminer leur forme originelle,
- déterminer des séquences techniques de production (par ex., une séquence de débitage dans le cas d’objet de pierre taillée), et
- estimer la validité et la robustesse de distinctions entre unités spatiales et leur possible mélange qui serait du à des processus pré- ou post-dépositionnels.
Ce type d’analyse est employé de longue date pour ce troisième point, et les méthodes ont fait l’objet de nombreux perfectionnements (pour un survol, voir Cziesla et al. 1990, Schurmans & Debie 2007).
Ces méthodes reposent sur la comparaison du nombre de relations de remontage entre différentes les unités spatiales et au sein de ces unités.
Cependant, il a été démontré que se limiter à tenir compte du nombre de relations sans considérer leur topologie peut conduire à des interprétations trompeuses.
Une méthode, appelée TSAR (Topological Study of Archaeological Refitting), a été développée pour surmonter ce problème, employant les moyens de la théorie des graphes pour modéliser la topologie des relations de remontage entre fragments (Plutniak 2021b, Plutniak 2022b).
Cette approche renouvelée permet de distinguer les cas ambigus, et est beaucoup plus robuste et moins sensible au manque d’informations que les méthodes basées sur le décompte. Cela rend possible une évaluation plus précise de la fiabilité des limites reconnues entre unités spatiales.
Archeofrag est un package R (R core team 2021) implémentant la méthode TSAR (Plutniak 2022a).
Le package : contexte et motivations
Au cours des deux dernières décennies, l’usage de R en archéologie s’est accru lentement, quoique régulièrement. Cependant, le développement de packages R pour des besoins archéologiques spécifiques est un phénomène plus récent encore. Concernant l’analyse spatiale archéologique, en particulier, seuls quelques packages sont disponibles, notamment pour l’analyse stratigraphique :
stratigraphr: un package dans sa première phase de développement, dédié à la visualisation et à l’analyse des stratigraphies sous forme de graphes dirigés (matrices de Harris).tabula: un package générique permettant de visualiser des décomptes d’objets et permettant également de comparer des couches (Frerebeau 2019).recexcavAAR: un package pour la reconstruction 3D et l’analyse de fouille (Schmid & Serbe 2017).archaeoPhases: un package pour l’analyse Bayésienne des chronologies archéologiques et la définition de phases (Philippe & Vibet 2020).
Archeofrag complète cette série de packages en apportant des méthodes particulières à l’analyse des remontages.
Fonctionnalités du package
Archeofrag repose principalement sur le package igraph pour l’analyse de graphes (Csárdi & Nepusz 2006) ainsi que sur certaines fonctions du package RBGL (Carey et al. 2020).
Il inclut un jeu de données illustratif (Plutniak 2021a) contenant des données de remontages de potteries trouvées lors de fouilles menées à l’abri sous roche Liang Abu, à Bornéo (Plutniak et al. 2016).
Archeofrag comprend six principaux ensembles de fonctions :
- Gestion de données : création, vérification, et transformation de graphes de fragmentation (y compris la pondération des relations à partir des propriétés topologiques des sommets et, optionnellement, la taille et des fragments et la distance entre leurs lieux de découverte dans l’espace du site) ;
- Visualisation : représentation de graphes de fragmentation sous la forme de diagrammes nœuds-arêtes ;
- Statistiques relatives aux limites : décompte des relations dans et entre deux unités spatiales, mesure de leur cohésion (cohesion) et de leur mélange (admixture) ;
- Statistiques relatives aux unités spatiales : caractérisation de la topologie d’un ensemble donné de relations de remontage (par ex. une couche) ;
- Simulation : simulation de graphes de fragmentation artificiels, simulation de leur altération (par ex. des données manquantes) ; comparaison d’un graphe empirique avec des graphes simulés similaires et renvoi des résultats dans un format commode et lisible.
- Analyse des similarités : outre l’analyse topologique des remontages, des fonctions permettent d’analyser les relations de similitude, qui concernent des fragments considérés comme partageant suffisamment de caractéristiques communes (motif, matière, inclusions, etc.) pour affirmer qu’ils faisaient partie du même objet initial.
Format des données
Archeofrag est destiné à être utilisé avec deux sources de données, à savoir les données empiriques de l’utilisateur et les données générées artificiellement en utilisant la fonction de simulation. Les données de l’utilisateur doivent être réparties dans différents tableaux :
- Tableau des fragments : chaque ligne contient l’identifiant unique du fragment, son unité spatiale et, optionnellement, des informations supplémentaires ;
- Tableau des connexions : une liste des relations avec, pour chaque ligne, les identifiants des deux fragments liés ;
- Tableau des similarités (optionnel) : chaque ligne contient l’identifiant unique d’un fragment et l’identifiant de l’ensemble de fragments similaires auquel il appartient.
| id | fragment 1 | fragment 2 |
|---|---|---|
| 1 | A | B |
| 2 | C | D |
| 3 | D | E |
| 4 | E | C |
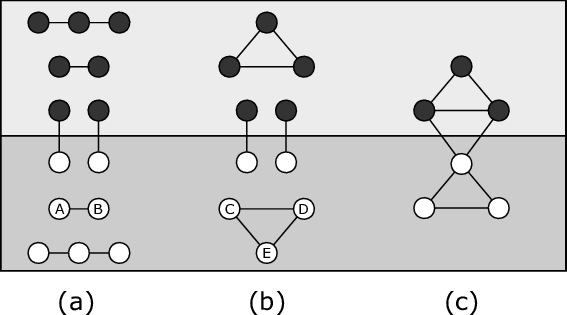
Tableau 1 : Enregistrement des relations de connexion entre fragments (illustrées sur la figure).
Le package inclut des fonctions permettant de générer des résumés statistiques sur un graphe de fragmentation et d’extraire des sous-graphes spécifiques (par couche, par taille, etc.).
Visualisation de graphes de fragmentation
Les graphes de fragmentation sont représentés sous forme de diagrammes nœuds–arêtes. Pour les graphes ne comportant que deux unités spatiales et des relations de connexion, les nœuds sont positionnés dans la partie supérieure et inférieure du diagramme en fonction de leur unité spatiale d’appartenance.
Statistiques relatives aux limites : mesure de la cohésion et du mélange de deux unités spatiales
Évaluer la pertinence de la distinction entre unités spatiales et mesurer leur cohésion constitue le premier objectif du package Archeofrag. L’évaluation suit une procédure en trois étapes, mises en œuvre dans trois fonctions complémentaires :
- Pondérer les arêtes. Trois paramètres peuvent être combinés : la topologie des relations de connexion (nécessaire), la taille des deux fragments connectés (optionnel), et la distance spatiale entre les lieux où ils ont été trouvés (optionnel). Les paramètres optionnels reposent sur l’hypothèse que deux grands fragments trouvés loin l’un de l’autre suggèrent davantage de perturbations dans le site que deux petits fragments trouvés proches l’un de l’autre ; voir une application et des détails dans (Caro et al. 2022).
- Mesure de la cohésion interne de chaque unité spatiale (intuitivement, la mesure dans laquelle elles « adhèrent » à elles-mêmes).
- Mesure du mélange de deux unités spatiales (une valeur calculée à partir des deux valeurs de cohésion).
Les valeurs de cohésion et de mélange sont calculées par paires d’unités spatiales. Les valeurs de cohésion sont comprises dans [0;1], avec des valeurs proches de 0 pour une cohésion faible et de 1 pour une cohésion élevée, leur somme n’étant jamais supérieure à 1 pour une paire d’unités spatiales. Les valeurs de mélange sont comprises dans [0;1].
Statistiques relatives aux unités spatiales : patterns de fragmentation, technologies, comportements humains
Le second objectif de la méthode TSAR implémentée dans Archeofrag est de caractériser les unités spatiales sur la base des propriétés topologiques des relations de connexion entre les fragments que ces unités contiennent.
Plusieurs mesures et fonctions sont prévues à cet effet, sélectionnées pour leur pertinence dans le contexte archéologique : le nombre de cycles, la longueur des plus courts chemins et le diamètre des composantes (une composante du graphe correspond à un objet initial).
L’interprétation archéologique des valeurs numériques obtenues dépend du type d’objet (lithique, poterie, etc.) et de leur caractère complet ou incomplet. Ces valeurs peuvent correspondre à des comportements spécifiques liés à la production ou à l’utilisation des objets (bris intentionnel), ou à des processus post-dépositionnels (bris naturel, dispersion). Cet aspect de la méthode TSAR fera l’objet de développements futurs.
Simulation de graphes de fragmentation
La fonction de simulation génère un ensemble de fragments connectés dispersés dans une ou deux unités spatiales (pour plus de détails, voir Plutniak 2021). Cette fonction peut être contrôlée avec plusieurs paramètres :
- Nombre d’objets ou de fragments initiaux.
- Nombre final de fragments.
- Nombre final de relations de connexion.
- Proportion de fragments dans chaque unité spatiale, avant les processus post-dépositionnels.
- Proportion d’objets dans chaque unité spatiale.
- Proportion de fragments susceptibles de se déplacer d’une unité spatiale à l’autre.
- Unités spatiales auxquelles la perturbation doit être appliquée (uniquement aux fragments de l’unité spatiale 1 ou de l’unité spatiale 2, ou les deux).
- Mesure dans laquelle, la fragmentation doit tendre à concerner des objets ayant déjà été fragmentés.
- Nombre d’unités spatiales hypothétiques initiales.
- Contraindre ou non les graphes générés à être planaires.
Contraindre les graphes simulés à être planaires a l’intérêt de correspondre à la fragmentation observée dans des cas archéologiques fréquents (par exemple, des poteries aux formes simples, de petits ensembles de remontages). Cependant, le temps d’exécution de cette fonction est doublé lorsque cette contrainte est appliquée.
Ressources et exemples
Archeofrag est disponible sur le CRAN et le code de développement est déposé sur Github.
Une Vignette et une application Shiny illustrent les fonctionnalités du package.
À l’heure de cette publication, Archeofrag a été appliqué à deux sites archéologiques :
- l’abri sous roche Liang Abu, en Indonésie (Plutniak 2021b, Plutniak et al. 2022),
- la grotte du Taï, en France (Caro et al. 2022).
Bibliographie
- Carey, Vince, Li Long & R. Gentleman. 2020. RBGL: An Interface to the BOOST Graph Library. DOI: 10.18129/B9.bioc.RBGL.
- Caro, Joséphine, Claire Manen, Agathe Baux & Sébastien Plutniak. 2022. “Les productions céramiques du Néolithique ancien et moyen : approches céramo-stratigraphique, technologique et morpho-stylistique.” In Claire Manen (dir.), Le Taï (Remoulins – Gard). Premières sociétés agropastorales du Languedoc méditerranéen (6e–3e millénaire avant notre ère), p. 616–687. Toulouse : Archives d’Écologie Préhistorique.
- Csárdi, Gábor & Tamás Nepusz. 2006. “The Igraph Software Package for Complex Network Research.” InterJournal 1695 (5):1–9. http://igraph.org.
- Cziesla, Erwin, Sabine Eickhoff, Nico Arts, & Doris Winter (dir.). 1990. The Big Puzzle: International Symposium on Refitting Stone Artefacts. Bonn: Holos.
- Frerebeau, Nicolas. 2019. “Tabula: An R Package for Analysis, Seriation, and Visualization of Archaeological Count Data.” Journal of Open Source Software 44 (4):1821. DOI: 10.21105/joss.01821.
- Philippe, Anne & Marie-Anne Vibet. 2020. “Analysis of Archaeological Phases Using the R Package Archaeophases.” Journal of Statistical Software 93. DOI: 10.18637/jss.v093.c01.
- Plutniak, Sébastien. 2021a. “Refitting Pottery Fragments from the Liang Abu Rockshelter, Borneo.” Zenodo. DOI: 10.5281/zenodo.4719577.
- Plutniak, Sébastien. 2021b. “The Strength of Parthood Ties. Modelling Spatial Units and Fragmented Objects with the Tsar Method – Topological Study of Archaeological Refitting.” Journal of Archaeological Science 136:105501. DOI: 10.1016/j.jas.2021.105501.
- Plutniak, Sébastien. 2022a. Archeofrag: An R Package for Refitting and Spatial Analysis in Archaeology. Zenodo. DOI: 10.5281/zenodo.6912425.
- Plutniak, Sébastien. 2022b. “L’analyse topologique des remontages archéologiques: la méthode TSAR et le package R archeofrag.” Bulletin de la Société préhistorique française 119 (1):110–13. HAL: hal-03631468
- Plutniak, Sébastien, Asftolfo Araujo, Adhi Agus Oktaviana, Bambang Sugiyanto, Jean-Michel Chazine & François-Xavier Ricaut. 2022. “Mainland-Coastal Interactions in East Borneo: Inter-Site Comparison and Bayesian Chronological Models of Two Late Pleistocene-Holocene Sequences (Liang Abu and Kimanis Rock Shelters).” Journal of Island and Coastal Archaeology. DOI: 10.1080/15564894.2022.2108947.
- Plutniak, Sébastien, Astolfo Araujo, Simon Puaud, Jean-Georges Ferrié, Adhi Agus Oktaviana, Bambang Sugiyanto, Jean-Michel Chazine, & François-Xavier Ricaut. 2016. “Borneo as a Half Empty Pot: Pottery Assemblage from Liang Abu, East Kalimantan.” Quaternary International 416:228–42. DOI: 10.1016/j.quaint.2015.11.080.
- R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org.
- Schmid, Clemens, & Benjamin Serbe. 2017. RecexcavAAR: 3D Reconstruction of Archaeological Excavations. https://CRAN.R-project.org/package=recexcavAAR.
- Schurmans, Utsav & Marc De Bie (dir.). 2007. Fitting Rocks: Lithic Refitting Examined. Oxford: Archaeopress.